Computing optimal road trips on a limited budget

About a year ago, I wrote an article introducing the concept of optimizing road trips using a combination of genetic algorithms and Google Maps. During that time, I've given some thought to how I could make that algorithm more useful to folks looking to plan their summer road trips.

One thought that struck me was that the road trips I created before were quite grandiose---spanning entire states or even most of Europe---such that only people who had some savings and were able to take a month off of work could even hope to go on one of the trips. In reality, most of us have budgetary constraints on our road trips: we can only spend so much money, or we only have so much time off before we have to get back to work.

In this article, I'm going to expand on the idea of optimizing road trips by introducing multi-objective Pareto optimization to the algorithm. I'll briefly describe how Pareto optimization works, and how it helps us optimize road trips on a limited budget.

Note: If you're not interested in the technical details of the project, skip down to the 48 U.S. state capitols in 8 1/2 days section.

Planning the road trip: U.S. state capitols

For this road trip, there is one goal: to take a picture at as many U.S. state capitols as possible. (Bonus points for entertaining or themed pictures!)

We will travel only by car, so that rules out Alaska (too far away) and Hawaii (requires a plane flight) and leaves us with the 48 contiguous states (excluding D.C.).

Whenever possible, we will avoid routes that require us to travel through foreign countries, as entering/leaving the country requires a passport and border control tends to slow things down.

Lastly, to clarify: The goal is to visit the capitol buildings, not the city the buildings are located in (i.e., state capitals). That said, by going on this road trip we're in for an epic journey and some beautiful architecture.

Image credit: Daniel Mennerich

Recap: Optimizing road trips

With the list of U.S. state capitols in hand, the next step is to find the "true" distance between all of the capitols by car. Since we can't just drive a straight line between every capitol---driving by car has this pesky limitation of having to stay on roads---we needed to find the shortest route by road between every capitol.

If you've ever used Google Maps to get the directions between two addresses, that's basically what we have to do here. Except this time, we need to look up 2,256 directions to get the "true" distance between all 48 state capitols---a monumental task if we have to do it by hand. Thankfully, the Google Maps API makes this information freely available, so all it takes is a short Python script to calculate the distance and time driven for all 2,256 routes between the 48 capitols.

Now with the 2,256 capitol-capitol distances, our next step is to approach the task as a traveling salesman problem: We need to order the list of capitols such that the total distance traveled between them is as small as possible if we visited them in order. This means finding the route that backtracks as little as possible, which is especially difficult when visiting Florida and the Northeast.

If you've read my Where's Waldo? article, you're already aware of how difficult it can be to solve route optimization problems like this one. With 48 landmarks to put in order, we would have to exhaustively evaluate 1.24 x 10⁶¹ possible routes to find the shortest one.

To provide some context: If you started computing this problem on your home computer right now, you'd find the optimal route in about 3.98 x 10⁴⁹ years---long after the Sun has entered its red giant phase and devoured the Earth. This complication is why Google Map's route optimization service only optimizes routes of up 10 waypoints, and the best free route optimization service only optimizes 20 waypoints unless you pay them a lot of money to dedicate some bigger computers to it.

The traveling salesman problem is so notoriously difficult to solve that even xkcd poked fun at it:

Clearly, we need a smarter solution if we want to take this road trip in our lifetime. Thankfully, the traveling salesman problem has been well-studied over the years and there are many ways for us to solve it in a reasonable amount of time.

If we're willing to accept that we don't need the absolute best route between all of the capitols, then we can turn to smarter techniques such as genetic algorithms to find a solution that's good enough for our purposes. Instead of exhaustively looking at every possible solution, genetic algorithms start with a handful of random solutions and continually tinkers with these solutions---always trying something slightly different from the current solutions and keeping the best ones---until they can't find a better solution any more.

I've included a visualization of a genetic algorithm optimizing one road trip below.

Multi-objective Pareto optimization

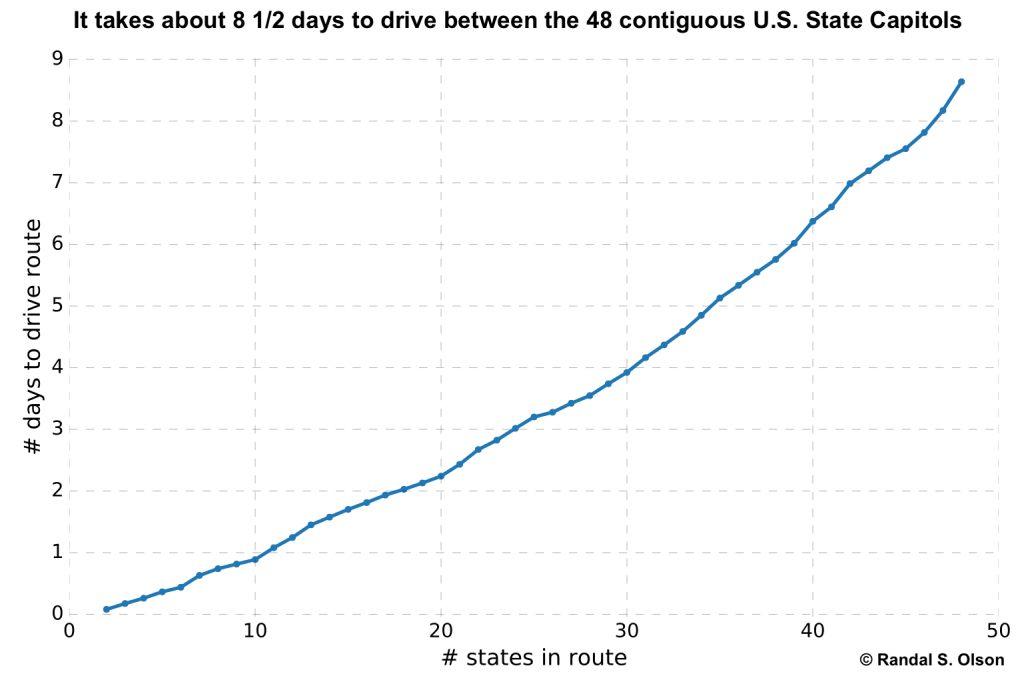
Normally in optimization problems, we want to maximize or minimize one criteria: Maximize how much money we make, or minimize the chance of an accident occurring. In multi-objective Pareto optimization, we can simultaneously optimize many criteria---for example, maximizing how many states we visit, while at the same time minimizing the total time we spend driving for the road trip.

In the chart below, each dot corresponds to one road trip. Watch as the genetic algorithm simultaneously optimizes 48 road trips.

What's particularly useful about Pareto optimization is that at the end of the optimization process, we have a Pareto front to choose from that lists the trade-offs between what we're trying to optimize. In the above chart, we see that the more states we visit, the longer the trip will take. If we only have 2 days to take a trip, for example, the Pareto front provides a plethora of trips to choose from: Maybe we should visit only a few capitols and have plenty of time to explore them, or perhaps we should visit as many capitols as possible in 2 days. The choice is ours.

In the animated map below, I've visualized all 48 of the optimized routes from the Pareto optimization process. Notice how each route differs slightly, for example, the optimized route that reaches 7 capitols is fairly different from the optimized route that reaches 8 capitols.

48 U.S. state capitols in 8 1/2 days

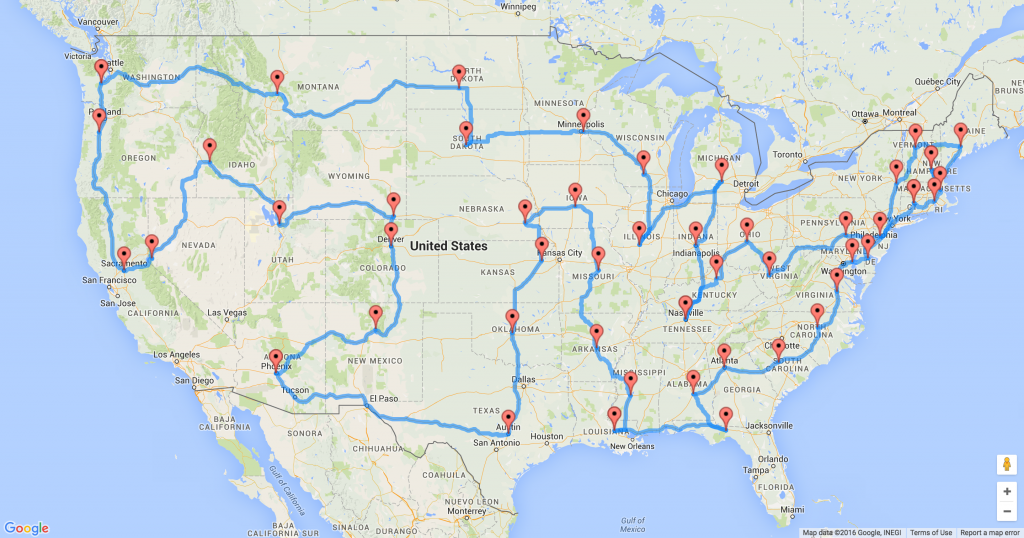
After running on my laptop for about 20 minutes, the genetic algorithm reached an optimized solution that makes a complete trip to all of the U.S. state capitols in only 13,310 miles (21,420 km) of driving. I've mapped that route below.

Assuming no traffic, this road trip will take about 8 1/2 days of driving in total, so you better bring a big water bottle. The best part is that this road trip is designed so that you can start anywhere on the route: As long as you follow the route from wherever you start, you'll hit every state capitol in the 48 contiguous U.S. states, and as an added bonus, you can even add Washington, D.C. to the route without adding any extra miles.

Here's the full list of capitols in order:

• State House, 107 North Main Street, Concord, NH 03303
• Maine State House, Augusta, ME 04330
• Vermont State House, 115 State Street, Montpelier, VT 05633
• New York State Capitol, State St. and Washington Ave, Albany, NY 12224
• New Jersey State House, Trenton, NJ 08608
• Pennsylvania State Capitol Building, North 3rd Street, Harrisburg, PA 17120
• West Virginia State Capitol, Charleston, WV 25317
• Ohio State Capitol, 1 Capitol Square, Columbus, OH 43215
• Kentucky State Capitol Building, 700 Capitol Avenue, Frankfort, KY 40601
• Tennessee State Capitol, 600 Charlotte Avenue, Nashville, TN 37243
• Indiana State Capitol, Indianapolis, IN 46204
• Michigan State Capitol, Lansing, MI 48933
• Illinois State Capitol, Springfield, IL 62756
• 2 E Main St, Madison, WI 53703
• Minnesota State Capitol, St Paul, MN 55155
• 500 E Capitol Ave, Pierre, SD 57501
• North Dakota State Capitol, Bismarck, ND 58501
• Montana State Capitol, 1301 E 6th Ave, Helena, MT 59601
• Washington State Capitol Bldg, 416 Sid Snyder Ave SW, Olympia, WA 98504
• Oregon State Capitol, 900 Court St NE, Salem, OR 97301
• L St & 10th St, Sacramento, CA 95814
• Nevada State Capitol, Carson City, NV 89701
• 700 W Jefferson St, Boise, ID 83720
• Utah State Capitol, Salt Lake City, UT 84103
• Wyoming State Capitol, Cheyenne, WY 82001
• 200 E Colfax Ave, Denver, CO 80203
• New Mexico State Capitol, Santa Fe, NM 87501
• Arizona State Capitol, 1700 W Washington St, Phoenix, AZ 85007
• Texas Capitol, 1100 Congress Avenue, Austin, TX 78701
• Oklahoma State Capitol, Oklahoma City, OK 73105
• 300 SW 10th Ave, Topeka, KS 66612
• Nebraska State Capitol, 1445 K Street, Lincoln, NE 68509
• Iowa State Capitol, 1007 E Grand Ave, Des Moines, IA 50319
• Missouri State Capitol, Jefferson City, MO 65101
• Arkansas State Capitol, 500 Woodlane Street, Little Rock, AR 72201
• 400-498 N West St, Jackson, MS 39201
• Louisiana State Capitol, Baton Rouge, LA 70802
• 402 S Monroe St, Tallahassee, FL 32301
• Alabama State Capitol, 600 Dexter Avenue, Montgomery, AL 36130
• Georgia State Capitol, Atlanta, GA 30334
• South Carolina State House, 1100 Gervais Street, Columbia, SC 29201
• North Carolina State Capitol, Raleigh, NC 27601
• Virginia State Capitol, Richmond, VA 23219
• Maryland State House, 100 State Cir, Annapolis, MD 21401
• Legislative Hall: The State Capitol, Legislative Avenue, Dover, DE 19901
• Connecticut State Capitol, 210 Capitol Ave, Hartford, CT 06106
• Rhode Island State House, 82 Smith Street, Providence, RI 02903
• Massachusetts State House, Boston, MA 02108

Here's the Google Maps for the road trip: [1] [2] [3] [4] [5]

(Note that Google Maps itself only allows 10 waypoints to be routed at a time, hence why there's multiple Maps links.)

10 U.S. state capitols in 24 hours

At this point, some of you might be scratching your heads. "Didn't you promise to stop showing us grandiose road trips, Randy?", I imagine you thinking.

This is where the Pareto optimization aspect comes in: If we look at the final Pareto front, we don't have to pick the 48-state road trip. We have a whole range of road trips to choose from.

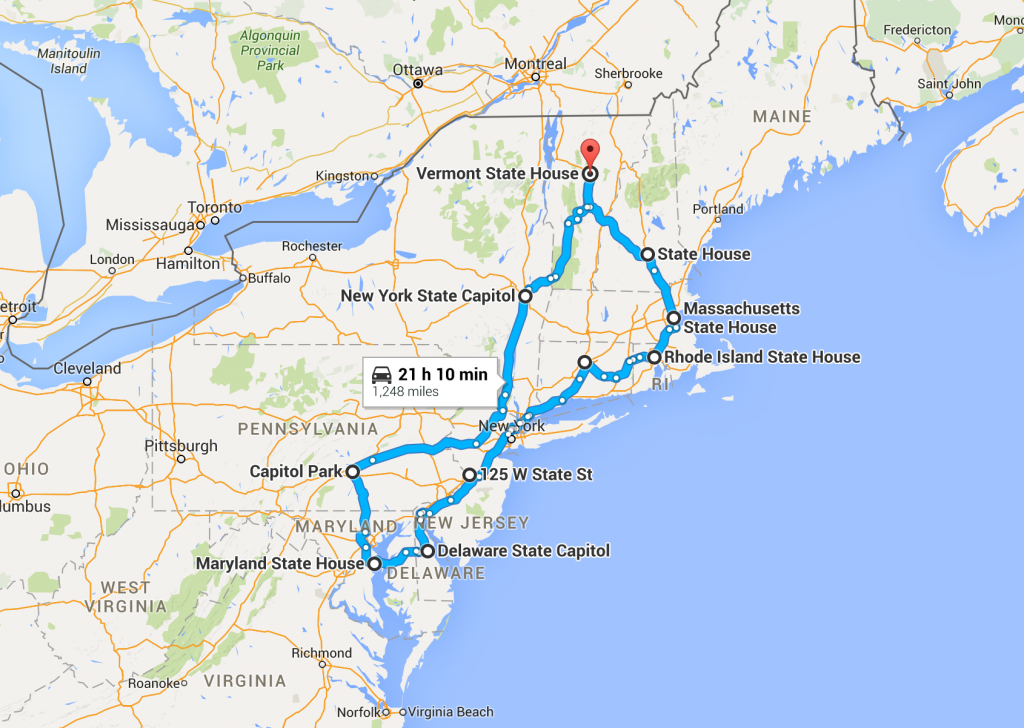
Let's say, for example, that we only have 24 hours to dedicate to the road trip. If that's the case, then we can look at the Pareto front above and see that we can reach 10 state capitols and arrive back home in less than 24 hours. That's pretty amazing to think that we can leave one morning, visit 10 state's capitols, and be back in time for breakfast the next day.

As you might expect, this road trip is in the Northeastern U.S.:

Here's the Google Map for the 24-hour road trip: [1]

If you want to look up the other road trips from the Pareto front, I've uploaded them on GitHub.

In theory, we can expand this idea to all kinds of budgets. If we only have $100 to spend on gas, we can add gas costs to the Pareto front. If we can only average $50/night on the hotel, we can add the average hotel cost at each stop to the Pareto front. And so on. At this point, the only limit is your imagination.

"This is awesome! How can I optimize my own road trip?"

If you were inspired by this article and want to make your own road trip, I've released the Python code I used in this project with an open source license and instructions for how to optimize your custom road trip. You can find the code here.

You should also check out Nathan Brixius' solution to this challenge using a technique from operations research. Nathan was kind enough to share all of his Python code as well.

Note: I don't make custom road trips upon request; I simply don't have the time. However, if you have a neat road trip idea that might be interesting to many people, please feel free to email me your idea.

Conclusions

I'm reminded of the quote:

The world is a book, and those who do not travel read only one page.

I hope that this article---through its odd mixture of travel, machine learning, and visualization---has inspired you to go out and embark on your own road trip. Whether it's a trip that a computer optimized in a few minutes or a trip that took you several weeks to hand-design, it only matters that you travel and experience the world from a fresh perspective.

Happy road tripping!