Growing up, there was a simple yet mesmerizing game that captured my attention every weekend known as the Original I.Q. Tester. This game, often found at the tables of family restaurants among syrup bottles and sticky menus, consisted of a wooden triangle filled with pegs, challenging players to jump pegs over each other until only one remained. The game became a ritualistic endeavor for me, especially on Sundays when I visited IHOP with my mom and step-dad on our weekly family outing. Amidst the aroma of pancakes and coffee, this game was one of my early forays into problem-solving and strategy, igniting a curiosity that has stayed with me into my later life and career.

Maybe you have fond memories of playing this game, too.

While cleaning out my mom's house earlier this month, an unexpected treasure surfaced from the depths of a moving box: an old Original I.Q. Tester. Had she kept it as a keepsake of our Sundays together, or did she intend to surprise me with it one day and then forgot? Either way, this rediscovery reignited my resolve to master the puzzle, not just through trial and error, but this time by harnessing the power of computation. For what other reason did I get this PhD, after all?

How difficult is Original I.Q. Tester?

To tackle the puzzle's challenge, I created a simulator for the puzzle in Python, a tool that modeled every conceivable starting position — each variation of the initial empty peg — and traced every potential path the game could follow. This digital experiment unearthed a staggering 7,335,390 possible outcomes, which highlights the game's deceptively complex nature. To put that number into context, even if I was able to play 10 unique paths every Sunday, it would have taken me over 14,000 years' worth of Sundays to play every possible path. That's a lot of pancakes!

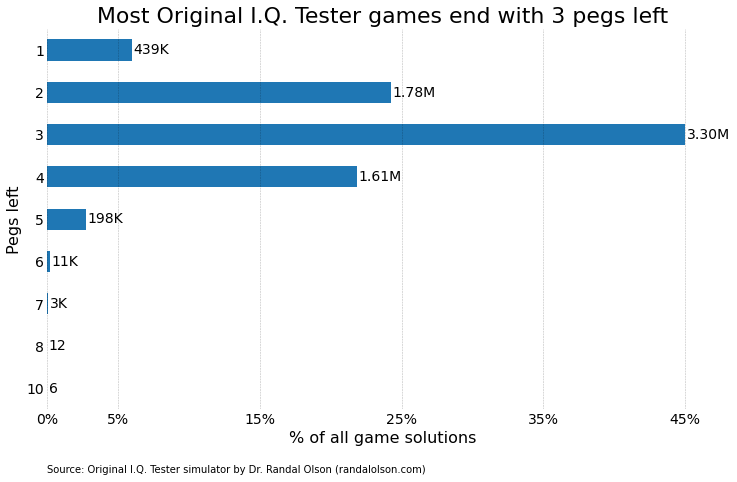
Interestingly, the data from my simulator revealed that about 94% of all possible games end with two or more pegs defiantly remaining on the board, a statistic that underscores the puzzle's difficulty and its knack for humbling even the most strategic minds — mine among them.

Where's the best starting point?

In my initial encounters with the I.Q. Tester, I instinctively chose to start with an empty peg somewhere in the center, often in the middle of the third row from the top, assuming this offered the greatest flexibility for interesting maneuvers. This intuition seemed logical, suggesting a wealth of strategic paths from the heart of the board.

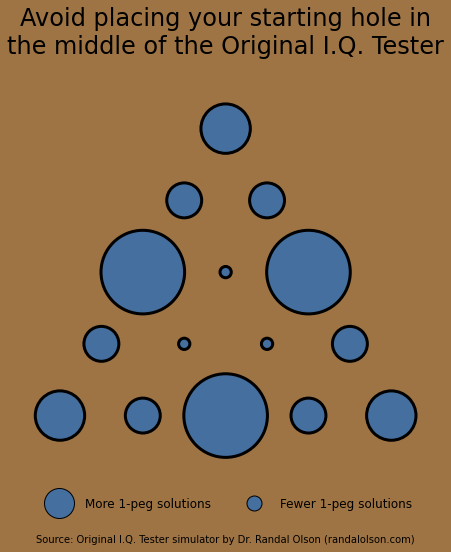
However, after rigorously analyzing every conceivable game trajectory through my simulator, I was amused — and admittedly a bit chagrined — to find that starting in the middle actually set the stage for the worst possible outcomes, dramatically limiting the paths that could lead to a single peg standing. The data compellingly pointed to the edges of the third row from the top and the center of the bottom row as the optimal starting points, revealing a counterintuitive strategy (for me) that significantly increases your chances of solving the puzzle.

What's a good jump strategy to reach 1 peg?

Next, I wanted to learn what sort of jump strategy worked best for the puzzle. In my early days, I oscillated between instinctive play, selecting jumps on a whim, and a more deliberate strategy, aiming to consolidate my pegs towards the board's center in hope of increasing the availability of subsequent jumps. This latter approach was grounded in a belief that a concentrated cluster of pegs would inherently offer more opportunities for strategic moves.

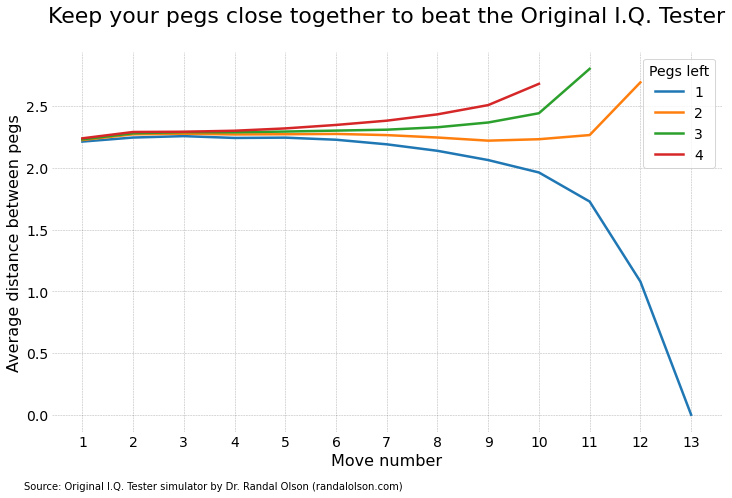
The data from my game-path analysis painted a clear picture: consistently opting for moves that draw pegs closer significantly boosts the likelihood of achieving the coveted outcome of a solitary peg standing. Conversely, the allure of seemingly strategic, yet ultimately divisive jumps proved to be a pitfall, as spreading the pegs across the board invariably diminishes your chances of success. Notably, early on it's fairly difficult to put this strategy into effect because the pegs are everywhere. That means you have to focus on eliminating one side of the triangle first so you can later concentrate the pegs on one side of the puzzle.

This revelation was a nod to my initial instincts, affirming that cohesion, not dispersion, was key to conquering the game's intricate puzzle. Just like so many things in life, right?

And sure enough, when I followed this strategy myself through a few games, I was finally able to end a game with a single peg. Victory at last!

Some example games

If you're curious what this strategy looks like when played out, here's one of the 439,000 game paths that lead to a single peg.

Board labels:
        A1
      B1  B2
    C1  C2  C3
  D1  D2  D3  D4
E1  E2  E3  E4  E5


Initial board state (1 = peg, 0 = empty):
    1     
   1 1    
  0 1 1   
 1 1 1 1  
1 1 1 1 1 


Move 1: A1 to C1
    0     
   0 1    
  1 1 1   
 1 1 1 1 
1 1 1 1 1 


Move 2: D1 to B1
    0     
   1 1    
  0 1 1   
 0 1 1 1  
1 1 1 1 1 


Move 3: C3 to C1
    0     
   1 1    
  1 0 0   
 0 1 1 1  
1 1 1 1 1 


Move 4: E5 to C3
    0     
   1 1    
  1 0 1   
 0 1 1 0  
1 1 1 1 0 


Move 5: B1 to D1
    0     
   0 1    
  0 0 1   
 1 1 1 0  
1 1 1 1 0 


Move 6: B2 to D4
    0     
   0 0    
  0 0 0   
 1 1 1 1  
1 1 1 1 0 


Move 7: E1 to C1
    0     
   0 0    
  1 0 0   
 0 1 1 1  
0 1 1 1 0 


Move 8: E3 to E5
    0     
   0 0    
  1 0 0   
 0 1 1 1  
0 1 0 0 1 


Move 9: C1 to E3
    0     
   0 0    
  0 0 0   
 0 0 1 1  
0 1 1 0 1 


Move 10: E2 to E4
    0     
   0 0    
  0 0 0   
 0 0 1 1  
0 0 0 1 1 


Move 11: E5 to E3
    0     
   0 0    
  0 0 0   
 0 0 1 1  
0 0 1 0 0 


Move 12: E3 to C3
    0     
   0 0    
  0 0 1   
 0 0 0 1  
0 0 0 0 0 


Move 13: C3 to E5
    0     
   0 0    
  0 0 0   
 0 0 0 0  
0 0 0 0 1

Similarly, if you want to see what the opposite of this strategy looks like, here's a typical game path that ends with 3 pegs on the board.

Board labels:
        A1
      B1  B2
    C1  C2  C3
  D1  D2  D3  D4
E1  E2  E3  E4  E5


Initial board state (1 = peg, 0 = empty):
    1     
   1 1    
  0 1 1   
 1 1 1 1  
1 1 1 1 1 


Move 1: C3 to C1
    1     
   1 1    
  1 0 0   
 1 1 1 1  
1 1 1 1 1 


Move 2: E3 to C3
    1     
   1 1    
  1 0 1   
 1 1 0 1  
1 1 0 1 1 


Move 3: D1 to D3
    1     
   1 1    
  1 0 1   
 0 0 1 1  
1 1 0 1 1 


Move 4: D4 to D2
    1     
   1 1    
  1 0 1   
 0 1 0 0  
1 1 0 1 1 


Move 5: B2 to D4
    1     
   1 0    
  1 0 0   
 0 1 0 1  
1 1 0 1 1 


Move 6: E2 to C2
    1     
   1 0    
  1 1 0   
 0 0 0 1  
1 0 0 1 1 


Move 7: B1 to D3
    1     
   0 0    
  1 0 0   
 0 0 1 1  
1 0 0 1 1 


Move 8: D4 to D2
    1     
   0 0    
  1 0 0   
 0 1 0 0  
1 0 0 1 1 


Move 9: C1 to E3
    1     
   0 0    
  0 0 0   
 0 0 0 0  
1 0 1 1 1 


Move 10: E4 to E2
    1     
   0 0    
  0 0 0   
 0 0 0 0  
1 1 0 0 1 


Move 11: E1 to E3
    1     
   0 0    
  0 0 0   
 0 0 0 0  
0 0 1 0 1

Finally, if you just want to feel better about yourself for never passing the 3-peg mark, here's one of the 6 ways to fail so spectacularly that you end up with 10 pegs left on the board and no valid jumps.

Board labels:
        A1
      B1  B2
    C1  C2  C3
  D1  D2  D3  D4
E1  E2  E3  E4  E5


Initial board state (1 = peg, 0 = empty):
    1     
   1 1    
  1 0 1   
 1 1 1 1  
1 1 1 1 1 


Move 1: E4 to C2
    1     
   1 1    
  1 1 1   
 1 1 0 1  
1 1 1 0 1 


Move 2: B1 to D3
    1     
   0 1    
  1 0 1   
 1 1 1 1  
1 1 1 0 1 


Move 3: E2 to C2
    1     
   0 1    
  1 1 1   
 1 0 1 1  
1 0 1 0 1 


Move 4: D3 to B1
    1     
   1 1    
  1 0 1   
 1 0 0 1  
1 0 1 0 1 

Take-aways

Embarking on this computational quest to solve the Original I.Q. Tester was not just an exercise in tryhardism or analytics; it was a bridge to the past for me, a connection to the cherished moments I used to spend with my mom. I found myself often thinking back to those Sunday mornings, her laughter and gentle encouragement mingling with the clatter of pegs while we talked about our upcoming week and I invariably moaned about something only a teenager would care about. I miss her deeply, yet through this project, I've found solace in the realization that our loved ones often leave us with puzzles — not just those of wood and pegs, but puzzles of the heart, teaching us about resilience, togetherness, and the beauty of simple shared moments. I hope this story inspires you to cherish the puzzles in your life, recognizing them as opportunities for growth, reflection, and a reminder of the bonds that, though unseen, forever hold us close to those we love.

Or, at the very least, you can impress someone with your newfound puzzle-solving skills.

If you'd like to chat puzzle strategy or even share your own memories, feel free to contact me anytime.