Statistical analysis made easy in Python with SciPy and pandas DataFrames

I finally got around to finishing up this tutorial on how to use pandas DataFrames and SciPy together to handle any and all of your statistical needs in Python. This is basically an amalgamation of my two previous blog posts on pandas and SciPy.

This is all coded up in an IPython Notebook, so if you want to try things out for yourself, everything you need is available on github: https://github.com/briandconnelly/BEACONToolkit/tree/master/analysis/scripts

Statistical Analysis in Python

In this section, we introduce a few useful methods for analyzing your data in Python. Namely, we cover how to compute the mean, variance, and standard error of a data set. For more advanced statistical analysis, we cover how to perform a Mann-Whitney-Wilcoxon (MWW) RankSum test, how to perform an Analysis of variance (ANOVA) between multiple data sets, and how to compute bootstrapped 95% confidence intervals for non-normally distributed data sets.

Python's SciPy Module

The majority of data analysis in Python can be performed with the SciPy module. SciPy provides a plethora of statistical functions and tests that will handle the majority of your analytical needs. If we don't cover a statistical function or test that you require for your research, SciPy's full statistical library is described in detail at: http://docs.scipy.org/doc/scipy/reference/tutorial/stats.html

Python's pandas Module

The pandas module provides powerful, efficient, R-like DataFrame objects capable of calculating statistics en masse on the entire DataFrame. DataFrames are useful for when you need to compute statistics over multiple replicate runs.

For the purposes of this tutorial, we will use Luis Zaman's digital parasite data set:

	from pandas import *
	
	# must specify that blank space " " is NaN
	experimentDF = read_csv("parasite_data.csv", na_values=[" "])
	
	print experimentDF
	
	[class 'pandas.core.frame.DataFrame']
	Int64Index: 350 entries, 0 to 349
	Data columns:
	Virulence           300  non-null values
	Replicate           350  non-null values
	ShannonDiversity    350  non-null values
	dtypes: float64(2), int64(1)

Accessing data in pandas DataFrames

You can directly access any column and row by indexing the DataFrame.

	# show all entries in the Virulence column
	print experimentDF["Virulence"]
	
	0     0.5
	1     0.5
	2     0.5
	3     0.5
	4     0.5
	...
	346   NaN
	347   NaN
	348   NaN
	349   NaN
	Name: Virulence, Length: 350

	# show the 12th row in the ShannonDiversity column
	print experimentDF["ShannonDiversity"][12]
	
	1.58981

You can also access all of the values in a column meeting a certain criteria.

	# show all entries in the ShannonDiversity column > 2.0
	print experimentDF[experimentDF["ShannonDiversity"] > 2.0]
	
	     Virulence  Replicate  ShannonDiversity
	8          0.5          9           2.04768
	89         0.6         40           2.01066
	92         0.6         43           2.90081
	96         0.6         47           2.02915
	...
	235        0.9         36           2.19565
	237        0.9         38           2.16535
	243        0.9         44           2.17578
	251        1.0          2           2.16044

Blank/omitted data (NA or NaN) in pandas DataFrames

Blank/omitted data is a piece of cake to handle in pandas. Here's an example data set with NA/NaN values.

	import numpy as np
	print experimentDF[np.isnan(experimentDF["Virulence"])]
	
		 Virulence  Replicate  ShannonDiversity
	300        NaN          1          0.000000
	301        NaN          2          0.000000
	302        NaN          3          0.833645
	303        NaN          4          0.000000
	...
	346        NaN         47          0.000000
	347        NaN         48          0.444463
	348        NaN         49          0.383512
	349        NaN         50          0.511329

DataFrame methods automatically ignore NA/NaN values.

	print "Mean virulence across all treatments:", experimentDF["Virulence"].mean()
	
	Mean virulence across all treatments: 0.75

However, not all methods in Python are guaranteed to handle NA/NaN values properly.

	from scipy import stats

	print "Mean virulence across all treatments:", stats.sem(experimentDF["Virulence"])
	
	Mean virulence across all treatments: nan

Thus, it behooves you to take care of the NA/NaN values before performing your analysis. You can either:

(1) filter out all of the entries with NA/NaN

	# NOTE: this drops the entire row if any of its entries are NA/NaN!
	print experimentDF.dropna()
	
	[class 'pandas.core.frame.DataFrame']
	Int64Index: 300 entries, 0 to 299
	Data columns:
	Virulence           300  non-null values
	Replicate           300  non-null values
	ShannonDiversity    300  non-null values
	dtypes: float64(2), int64(1)

If you only care about NA/NaN values in a specific column, you can specify the column name first.

	print experimentDF["Virulence"].dropna()
	
   0.5
   0.5
   0.5
   0.5
	...
  1
  1
  1
  1
	Name: Virulence, Length: 300

(2) replace all of the NA/NaN entries with a valid value

	print experimentDF.fillna(0.0)["Virulence"]
	
   0.5
   0.5
   0.5
   0.5
   0.5
	...
  0
  0
  0
  0
	Name: Virulence, Length: 350

Take care when deciding what to do with NA/NaN entries. It can have a significant impact on your results!

	print ("Mean virulence across all treatments w/ dropped NaN:",
		experimentDF["Virulence"].dropna().mean())
	
	print ("Mean virulence across all treatments w/ filled NaN:",
		experimentDF.fillna(0.0)["Virulence"].mean())
	
	Mean virulence across all treatments w/ dropped NaN: 0.75
	Mean virulence across all treatments w/ filled NaN: 0.642857142857

Mean of a data set

The mean performance of an experiment gives a good idea of how the experiment will turn out on average under a given treatment.

Conveniently, DataFrames have all kinds of built-in functions to perform standard operations on them en masse: `add()`, `sub()`, `mul()`, `div()`, `mean()`, `std()`, etc. The full list is located at: http://pandas.pydata.org/pandas-docs/stable/api.html#computations-descriptive-stats

Thus, computing the mean of a DataFrame only takes one line of code:

	from pandas import *
	
	print ("Mean Shannon Diversity w/ 0.8 Parasite Virulence =",
		experimentDF[experimentDF["Virulence"] == 0.8]["ShannonDiversity"].mean())
	
	Mean Shannon Diversity w/ 0.8 Parasite Virulence = 1.2691338188

Variance in a data set

The variance in the performance provides a measurement of how consistent the results of an experiment are. The lower the variance, the more consistent the results are, and vice versa.

Computing the variance is also built in to pandas DataFrames:

	from pandas import *
	
	print ("Variance in Shannon Diversity w/ 0.8 Parasite Virulence =",
		experimentDF[experimentDF["Virulence"] == 0.8]["ShannonDiversity"].var())
	
	Variance in Shannon Diversity w/ 0.8 Parasite Virulence = 0.611038433313

Standard Error of the Mean (SEM)

Combined with the mean, the SEM enables you to establish a range around a mean that the majority of any future replicate experiments will most likely fall within.

pandas DataFrames don't have methods like SEM built in, but since DataFrame rows/columns are treated as lists, you can use any NumPy/SciPy method you like on them.

	from pandas import *
	from scipy import stats
	
	print ("SEM of Shannon Diversity w/ 0.8 Parasite Virulence =",
		stats.sem(experimentDF[experimentDF["Virulence"] == 0.8]["ShannonDiversity"]))
	
	SEM of Shannon Diversity w/ 0.8 Parasite Virulence = 0.110547585529

A single SEM will usually envelop 68% of the possible replicate means and two SEMs envelop 95% of the possible replicate means. Two SEMs are called the "estimated 95% confidence interval." The confidence interval is estimated because the exact width depend on how many replicates you have; this approximation is good when you have more than 20 replicates.

Mann-Whitney-Wilcoxon (MWW) RankSum test

The MWW RankSum test is a useful test to determine if two distributions are significantly different or not. Unlike the t-test, the RankSum test does not assume that the data are normally distributed, potentially providing a more accurate assessment of the data sets.

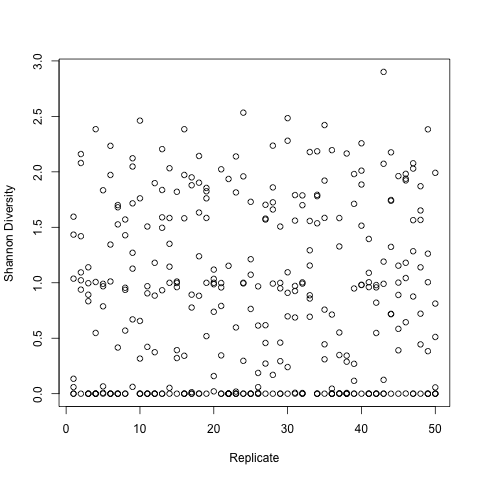
As an example, let's say we want to determine if the results of the two following treatments significantly differ or not:

	# select two treatment data sets from the parasite data
	treatment1 = experimentDF[experimentDF["Virulence"] == 0.5]["ShannonDiversity"]
	treatment2 = experimentDF[experimentDF["Virulence"] == 0.8]["ShannonDiversity"]
	
	print "Data set 1:\n", treatment1
	print "Data set 2:\n", treatment2
	
	Data set 1:
	0     0.059262
	1     1.093600
	2     1.139390
	3     0.547651
	...
	45    1.937930
	46    1.284150
	47    1.651680
	48    0.000000
	49    0.000000
	Name: ShannonDiversity
	Data set 2:
	150    1.433800
	151    2.079700
	152    0.892139
	153    2.384740
	...
	196    2.077180
	197    1.566410
	198    0.000000
	199    1.990900
	Name: ShannonDiversity

A RankSum test will provide a P value indicating whether or not the two distributions are the same.

	from scipy import stats
	
	z_stat, p_val = stats.ranksums(treatment1, treatment2)
	
	print "MWW RankSum P for treatments 1 and 2 =", p_val
	
	MWW RankSum P for treatments 1 and 2 = 0.000983355902735

If P <= 0.05, we are highly confident that the distributions significantly differ, and can claim that the treatments had a significant impact on the measured value.

If the treatments do not significantly differ, we could expect a result such as the following:

	treatment3 = experimentDF[experimentDF["Virulence"] == 0.8]["ShannonDiversity"]
	treatment4 = experimentDF[experimentDF["Virulence"] == 0.9]["ShannonDiversity"]
	
	print "Data set 3:\n", treatment3
	print "Data set 4:\n", treatment4
	
	Data set 3:
	150    1.433800
	151    2.079700
	152    0.892139
	153    2.384740
	...
	196    2.077180
	197    1.566410
	198    0.000000
	199    1.990900
	Name: ShannonDiversity
	Data set 4:
	200    1.036930
	201    0.938018
	202    0.995956
	203    1.006970
	...
	246    1.564330
	247    1.870380
	248    1.262280
	249    0.000000
	Name: ShannonDiversity

	# compute RankSum P value
	z_stat, p_val = stats.ranksums(treatment3, treatment4)

	print "MWW RankSum P for treatments 3 and 4 =", p_val
	
	MWW RankSum P for treatments 3 and 4 = 0.994499571124

With P > 0.05, we must say that the distributions do not significantly differ. Thus changing the parasite virulence between 0.8 and 0.9 does not result in a significant change in Shannon Diversity.

One-way analysis of variance (ANOVA)

If you need to compare more than two data sets at a time, an ANOVA is your best bet. For example, we have the results from three experiments with overlapping 95% confidence intervals, and we want to confirm that the results for all three experiments are not significantly different.

	treatment1 = experimentDF[experimentDF["Virulence"] == 0.7]["ShannonDiversity"]
	treatment2 = experimentDF[experimentDF["Virulence"] == 0.8]["ShannonDiversity"]
	treatment3 = experimentDF[experimentDF["Virulence"] == 0.9]["ShannonDiversity"]
	
	print "Data set 1:\n", treatment1
	print "Data set 2:\n", treatment2
	print "Data set 3:\n", treatment3
	
	Data set 1:
	100    1.595440
	101    1.419730
	102    0.000000
	103    0.000000
	...
	146    0.000000
	147    1.139100
	148    2.383260
	149    0.056819
	Name: ShannonDiversity
	Data set 2:
	150    1.433800
	151    2.079700
	152    0.892139
	153    2.384740
	...
	196    2.077180
	197    1.566410
	198    0.000000
	199    1.990900
	Name: ShannonDiversity
	Data set 3:
	200    1.036930
	201    0.938018
	202    0.995956
	203    1.006970
	...
	246    1.564330
	247    1.870380
	248    1.262280
	249    0.000000
	Name: ShannonDiversity

	# compute one-way ANOVA P value	
	from scipy import stats
		
	f_val, p_val = stats.f_oneway(treatment1, treatment2, treatment3)
	
	print "One-way ANOVA P =", p_val
	
	One-way ANOVA P = 0.381509481874

If P > 0.05, we can claim with high confidence that the means of the results of all three experiments are not significantly different.

Bootstrapped 95% confidence intervals

Oftentimes in wet lab research, it's difficult to perform the 20 replicate runs recommended for computing reliable confidence intervals with SEM.

In this case, bootstrapping the confidence intervals is a much more accurate method of determining the 95% confidence interval around your experiment's mean performance.

Unfortunately, SciPy doesn't have bootstrapping built into its standard library yet. However, there is already a scikit out there for bootstrapping. Enter the following command to install it:

sudo easy_install scikits.bootstrap

Bootstrapping 95% confidence intervals around the mean with this function is simple:

	# subset a list of 10 data points
	treatment1 = experimentDF[experimentDF["Virulence"] == 0.8]["ShannonDiversity"][:10]
	
	print "Small data set:\n", treatment1
	
	Small data set:
	150    1.433800
	151    2.079700
	152    0.892139
	153    2.384740
	154    0.006980
	155    1.971760
	156    0.000000
	157    1.428470
	158    1.715950
	159    0.000000
	Name: ShannonDiversity

	import scipy
	import scikits.bootstrap as bootstrap

	# compute 95% confidence intervals around the mean
	CIs = bootstrap.ci(data=treatment1, statfunction=scipy.mean)

	print "Bootstrapped 95% confidence intervals\nLow:", CIs[0], "\nHigh:", CIs[1]
	
	Bootstrapped 95% confidence intervals
	Low: 0.659028048 
	High: 1.722468024

Note that you can change the range of the confidence interval by setting the alpha:

	# 80% confidence interval
	CIs = bootstrap.ci(treatment1, scipy.mean, alpha=0.2)
	print "Bootstrapped 80% confidence interval\nLow:", CIs[0], "\nHigh:", CIs[1]
	
	Bootstrapped 80% confidence interval
	Low: 0.827291024 
	High: 1.5420059

And also modify the size of the bootstrapped sample pool that the confidence intervals are taken from:

	# bootstrap 20,000 samples instead of only 10,000
	CIs = bootstrap.ci(treatment1, scipy.mean, n_samples=20000)
	print ("Bootstrapped 95% confidence interval w/ 20,000 samples\nLow:",
		CIs[0], "\nHigh:", CIs[1])
	
	Bootstrapped 95% confidence interval w/ 20,000 samples
	Low: 0.644756972 
	High: 1.7071459

Generally, bootstrapped 95% confidence intervals provide more accurate confidence intervals than 95% confidence intervals estimated from the SEM.