A short guide to using statistics in Evolutionary Computation
Published on July 20, 2013 by Dr. Randal S. Olson
95% confidence interval benchmark testing evolutionary computation performance comparison statistics
9 min READ
A couple weeks ago, I attended the Genetic and Evolutionary Computation Conference (GECCO) for the first time. While I was perusing through the workshops and tutorials available in the first couple days of the conference, I noticed something peculiar: There was an introductory tutorial on statistics. "Why are they teaching basic stats at such a prestigious conference?," I wondered. "Shouldn't most Evolutionary Computation (EC) researchers here know basic stats and how important it is?"
Once I sat through the first day of presentations, I quickly realized why that tutorial was offered: At least half of the presentations were lacking statistics!
That's when I remembered that Computer Scientists aren't really taught statistics. During my undergraduate CS degree, I took an intro stats course during Freshman year that I was happy to banish from my mind after the final exam. During my graduate CS training, I learned a little bit about stats in my data mining course, but no teachers ever stressed stats as a method for inference from experimental data, nor did they talk about 95% confidence intervals and P-values. In fact, the only reason I learned about using stats was because of my interdisciplinary training in biological studies, where researchers live and die by making statistical inferences from their data.
Since not everyone can attend the GECCO workshops, and assuming my CS training is representative of most CS training nowadays, I've written a short guide to explain why statistics is important in EC and how to use basic statistics in EC research.
Why statistics is important in EC
EC is inherently random
In core Computer Science research, we rely on proofs and establishing best- and worst-case scenarios (i.e., performance boundaries) to scientifically validate and compare our work. For deterministic algorithms, that works fine. However, we have to keep in mind that EC uses an evolutionary process to guide the search, which means that the search process is inherently random to some degree. This is an important point to keep in mind because it means that two separate runs of the same evolutionary algorithm (with different random number seeds) can come up with completely different results.
The random nature of EC is even more important to keep in mind if we want to compare our evolutionary algorithm to another evolutionary algorithm. If we run both algorithms only once and compare their fitness over evolutionary time, chance is going to play a huge role in which algorithm appears to perform better. For example, if our evolutionary algorithm just happens to start near the best solution in the benchmark problem we're using, and the other evolutionary algorithm starts far away in the search space from the best solution, we might conclude that our algorithm performs better than the other algorithm. Such a case is represented in the graph below.
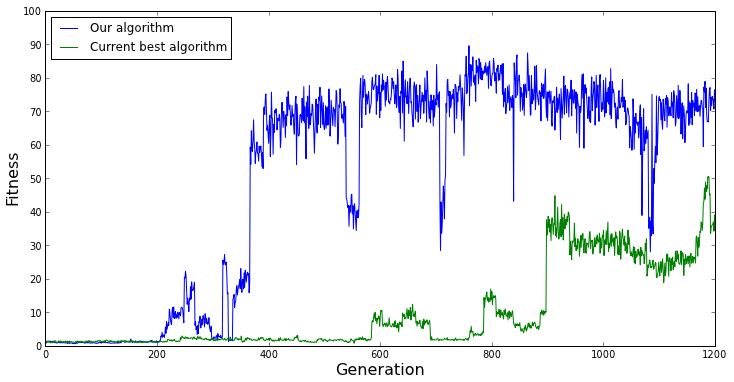
Graph showing the fitness over time for a single evolutionary run
However, the opposite situation might occur, and we could falsely conclude that our evolutionary algorithm performs worse. Such is the situation in the graph below.
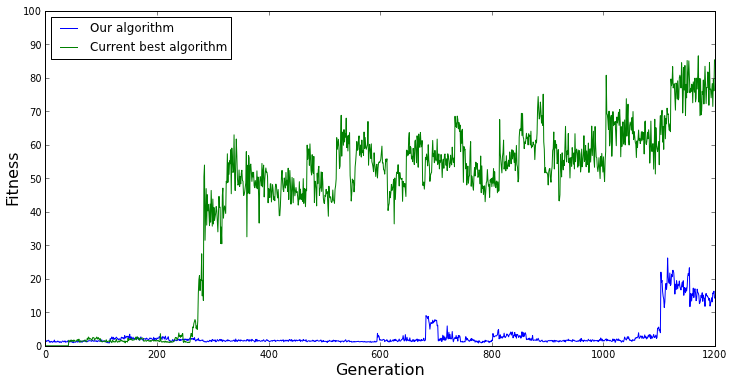
Graph showing the fitness over time for another single evolutionary run
Clearly, we can't make any comparisons between evolutionary algorithms based on individual runs.
Showing the average isn't enough
Some EC practitioners, privy to the above challenge, respond by running several replicates of each evolutionary algorithm (with different random number seeds) and show the average performance of each algorithm over time. This is typically what we see in EC conference presentations without statistics, where they plot the average fitness over evolutionary time.
The problem here is that the graph doesn't give us a sense of the range of performance of each algorithm. Remember, each evolutionary run will give a different result, which means that multiple replicates of an algorithm will perform differently. Without a sense for the range of each algorithm's performance, we can't really compare the two algorithms. The algorithms could be all over the place, sometimes performing well and other times performing poorly, or they could always perform well. Without a sense of the range, we don't know.
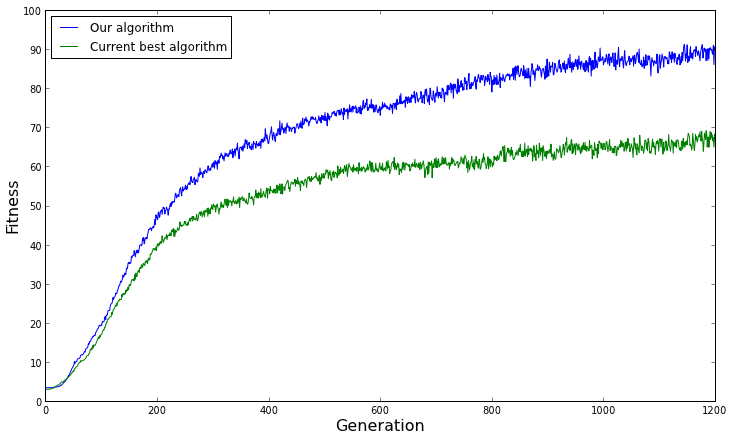
Graph showing the average fitness over time for 100 evolutionary runs
For example, look at the graph above. It looks like our evolutionary algorithm is performing better than the current best algorithm on average over many replicates, right? Let's show the 95% confidence intervals (estimated by showing 1.96 x standard error) to give a sense of the range of performance.
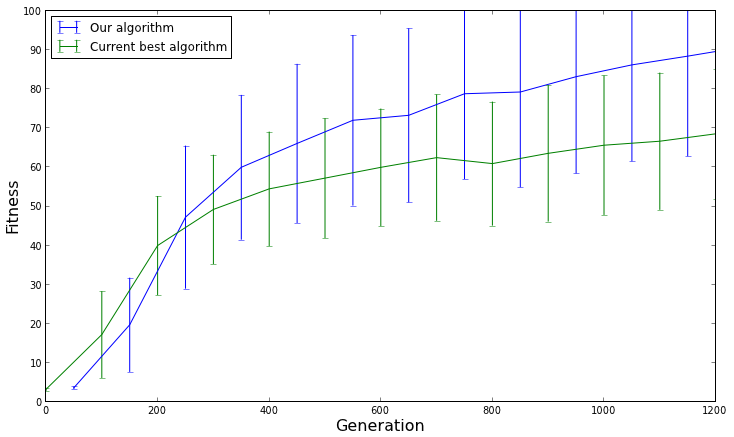
Graph showing the average fitness over time for 100 evolutionary runs with confidence intervals
The results don't look so different after all. The confidence intervals are wide, which means that the performance of the algorithms is all over the place. There's also quite a bit of overlap between the confidence intervals, which means that there isn't really a difference in performance between the two algorithms. The reason our algorithm seemed to perform better on average was only due to chance.
Statistics helps prevent false positives
In short, without showing some basic statistics, we could be misleading ourselves and others who follow up on our work. In the case above, if we hadn't looked at the 95% confidence intervals, we might have mistakenly claimed that our algorithm performs better than the current best algorithm. And that, if you ask me, is worse than not publishing at all.
Using statistics in Evolutionary Computation
Now that we're motivated to use statistics in Evolutionary Computation, there are just a few basic concepts we need to go over. Once we have these concepts down, we're ready to incorporate a basic, yet powerful statistical analysis into our EC research.
Replicates, replicates, and more replicates
First and foremost, if we want to get a sense for how our evolutionary algorithm is performing, we need to run it many times with different random number seeds. A general rule of thumb is that 30 replicates should be enough to get a broad idea of the evolutionary trends, then 100 or more replicates should be performed for the setup that is going to be published. In statistics, the Law of Large Numbers tells us that the more replicates we run, the closer we get to finding the true average performance, so more replicates is always better.
Standard error
As I alluded to earlier, the standard error gives us an idea of the range of our evolutionary algorithm's average performance. The higher the standard error, the larger the range of the performance, and vice versa. Standard error is computed with the equation:
where std deviation is a measure of how varied the fitness values are among our replicates and N is the number of replicates we ran. Every scientific computing library (R, matlab, SciPy, etc.) worth its salt has the standard error function built in, so we don't have to worry about coding it ourselves.
One interesting thing to note here is that we can make the standard error incredibly small by running thousands of replicates (N = 1000s), which means that we have a highly accurate measure of the evolutionary algorithm's average performance.
95% confidence intervals
Finally, from the standard error we can construct an estimated 95% confidence interval that shows us the range of our evolutionary algorithm's performance. If we were to run the algorithm multiple times again with different random number seeds, there is a 95% chance that the average performance of those replicates would fall within the confidence interval.
If we want to compare the performance of two algorithms, all we have to do is check whether the algorithm's 95% confidence intervals overlap. If they overlap, then there is a high chance that they perform the same. The more the confidence intervals overlap, the more likely the algorithms are to perform the same. On the other hand, if the 95% confidence intervals don't overlap, then the algorithm with the highest average performance performs significantly better.
One can imagine how this is useful for evolutionary computation research. Now we can make a statement such as, "We are confident that our evolutionary algorithm performs significantly better than the current best evolutionary algorithm at least 95% of the time," which is a scientifically powerful statement to make.
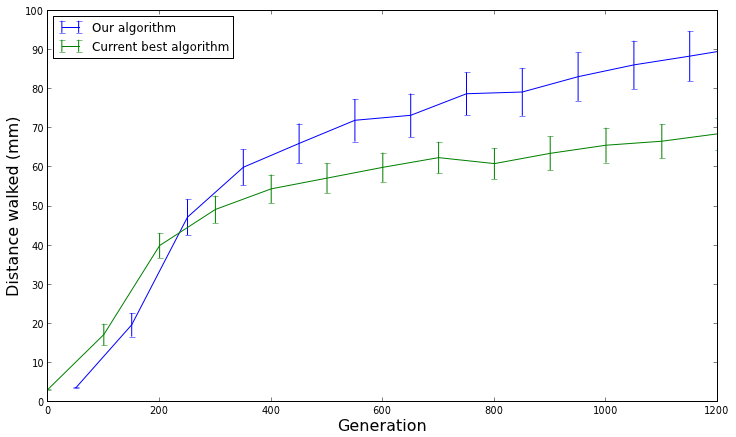
Graph showing the average fitness over time for 100 evolutionary runs with confidence intervals, highlighting significant differences
On top of that, because we show 95% confidence intervals, we can also think about whether our algorithm is realistically performing better than the other algorithm. For example, let's say we are comparing two evolutionary algorithms that evolve controllers for walking robots, and the graph above is a measure of how far the robots walked before falling over (in millimeters). Even if the confidence intervals don't overlap (indicating statistical significance), is walking 90mm really much better than walking 70mm? If you ask me, if the robot is only walking 90mm (~3.5 inches), neither algorithm is performing very well. Always remember to ask yourself: is the improved performance from the new algorithm realistically better?
We can compute an estimated 95% confidence interval by using the following equations:
[pmath]CI low = average - (1.96 * std error)[/pmath]
where the confidence interval ranges from CI low to CI high. CI low and CI high are the minimum and maximum points that we plot for the confidence intervals in the figures above. Again, scientific computing libraries already have functions built in to calculate 95% confidence intervals (both estimated & more precise versions), so don't worry about programming it.
Moving forward and changing the EC culture
Computing statistics on the performance of our evolutionary algorithms is incredibly simple, yet it allows us to make powerful statements about their relative performance. We should strive to build a culture of statistical analysis into the EC research community so we can avoid false positives on performance comparisons. That said, I hope this guide has convinced you that if you write or review a paper discussing an evolutionary algorithm, you will insist that at least basic statistics such as 95% confidence intervals be included before it is published.